PYTHAGOREISCHE ZAHLENTRIPEL

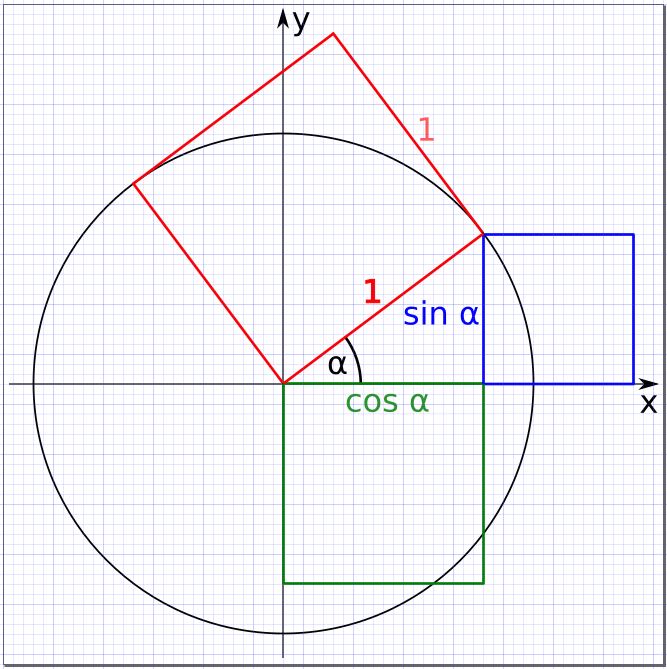
Wir alle kennen den Satz des Pythagoras. Natürlich kann man ihn auch so schreiben: x² + y² = 1

Pythagoreische Zahlentripel sind ganzzahlige Lösungen für die Pythagoras-Gleichung: a² + b² = c².

Dann sind x =a/c  und  y=b/c  rationale Zahlen.       Zum Beispiel 3² + 4² = 5².

a) Zeige, dass ein beliebig gewählter rationaler Punkt auf der x-Achse mit x >= 1, verbunden mit dem Punkt (0;1) auf dem Kreis, diesen stets in einem rationalen Punkt (xs;ys) schneidet.

b) Zeige weiterhin, dass durch diesen Schnittpunkt eindeutig ein weiteres pythagoreisches Zahlentripel erzeugt wird.

c) Welcher Punkt auf der x-Achse erzeugt das Tripel (3;4;5)?

d) Welches Zahlentripel wird vom Abszissenpunkt (5/2 ;0)  erzeugt?

Alle Einsendungen müssen eine vollständige Beschreibung des Lösungsweges enthalten und jeweils zum Ende des Monats beim Förderverein der Schule eingereicht werden: Diese E-Mail-Adresse ist vor Spambots geschützt! Zur Anzeige muss JavaScript eingeschaltet sein..                       

Der Preis für die am besten präsentierte richtige Lösung ist ein PYTHAGORAS BECHER: