DENKEN LOHNT SICH Nr. 8

Der polnische Mathematiker Wacław Franciszek Sierpiński erdachte 1915 eine iterative Dreieck-Konstruktion durch das Löschen der inneren Dreiecke der jeweiligen Restfigur. Die entstehende Figur führte zu einem der bekanntesten Fraktale der Chaosforschung und hat die Dimension log₂3.

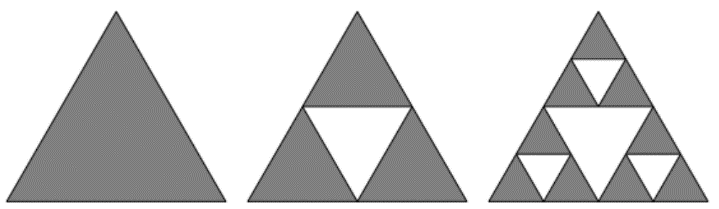
Betrachten wir jetzt nicht den Flächeninhalt, sondern nur die Sierpinski-Dreiecke als eine Widerstandsdraht-Konstruktion: Eine Seite des Sierpinski-Dreiecks der Stufe 0 habe eine Länge von genau 1 Meter und einen elektrischen Widerstand von genau 1 Ohm.

Bestimme den Widerstand der Sierpinski-Dreiecke zwischen 2 Ecken und die Länge des erforderlichen Drahtes für die gesamte Figur.

HINWEIS: In elektrischen Netzwerken kann man Punkte gleichen Potenzials (Spannung) verbinden, ohne die elektrischen Eigenschaften der Schaltung zu verändern. Informiere dich zusätzlich über die sogenannte „Stern-Dreiecks-Umwandlung“ bei Widerständen.

Alle Einsendungen müssen eine vollständige Beschreibung des Lösungsweges enthalten und jeweils zum Ende des Monats beim Förderverein der Schule eingereicht werden: Diese E-Mail-Adresse ist vor Spambots geschützt! Zur Anzeige muss JavaScript eingeschaltet sein..

Der Preis für die am besten präsentierten richtigen Lösungen in jeder Klassenstufe ist ein ...